Astronomical dials
The information on this page is useful for people who are interested
in construction of an astronomical clock, without the burden of the
mathematical background. Some knowledge of astronomical clocks and
dials is assumed. The template dials/ results of calculations for
geographic latitudes between 48 degrees and 56 degrees presented on this page,
may be downloaded free of charge, provided that you do so for your own
personal use. Any other usage requires explicit permission in
advance.
Background
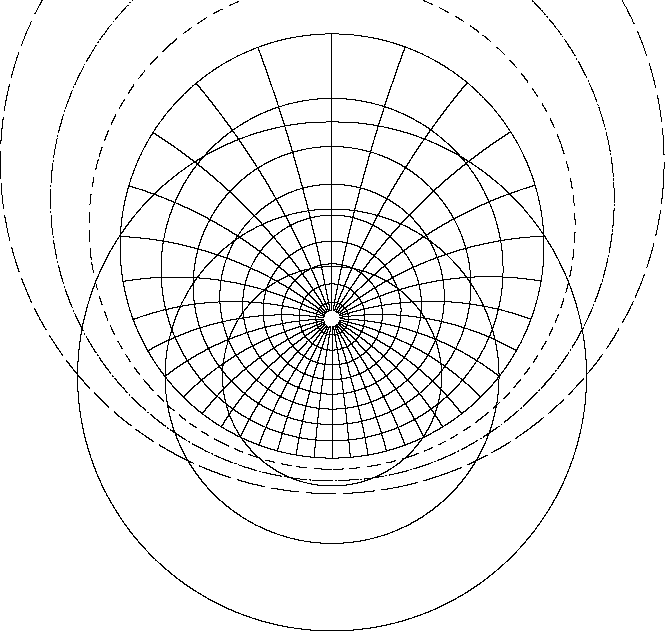
Some clocks indicate not only the time of day, but also the time of
sunrise, sunset, moonrise, moonset and even eclipses. These clocks
require special dials, such as those shown at the top of this page. In
principle, the curved lines are equivalent with the lines on a map of
the world: they indicate a coordinate grid (on the sky), in a map
projection which is particularly suitable for this purpose. To be more
specific, the coordinate grid is azimuth/elevation in a stereographic
projection from the South celestial pole. The three concentric circles
are projections of the equator, and the tropics of Cancer (inner
circle) and Capricorn (outer circle). At this point, I do not present
data for dials using the North stereographic projection.
Astronomical clocks were made hundreds of years ago. Today, such
clocks are still being (re)constructed. Some time ago, I was asked to
calculate these curves for a specific geographic latitude. As others
may benefit from these calculations, I present some results here.
The data on this page may be downloaded for private use only. Please
read this copyright notice. If you
decide to use any of these data, you accept that they are provided
without any warranty, and that you use them at your own risk. An email
of notification to

is appreciated. Further distribution of these data without prior written
consent is prohibited. Please read the description carefully.
About the data
The curves on the dials shown above are (segments of) circles. To
construct one of these circles, its centre and radius must be
specified. Although analytic expressions for these parameters exist, I
calculated them numerically because of the requirements of my personal
plotting program. You will find the numerical accuracy of the
calculations reflected in the numbers below. A comparison with
analytic results suggests a relative accuracy of the order of 1 in a
million for the coordinates I give in the files below. If the
equator is plotted as a circle with radius of 1 meter, the numerical
accuracy of the coordinates would be approxmimately 0.001 millimeter.
This is sufficient for any practical purpose, but some of the last digits
in the files below may not be significant. Note that I also give the
position of the ecliptic at some point in time, although the ecliptic is a
moving part of the clock, and should not be drawn on the dial!
Alternatively, you could use one of the PostScript or gif images
directly. If you do, be aware that a printer stretches the paper,
introducing significant deformations, which could be more important
than several degrees in geographic latitude.
Dials for different latitudes
Latitude 48 degrees 00 minutes also in 1.9 Mb Postscript or 15 kb gif
Latitude 49 degrees 00 minutes
Latitude 50 degrees 00 minutes
Latitude 50 degrees 30 minutes also in 1.9 Mb Postscript or 15 kb gif
Latitude 51 degrees 00 minutes
Latitude 51 degrees 30 minutes
Latitude 52 degrees 00 minutes also in 1.9 Mb Postscript or 15 kb gif
Latitude 52 degrees 30 minutes
Latitude 53 degrees 00 minutes
Latitude 53 degrees 30 minutes also in 1.9 Mb Postscript or 15 kb gif
Latitude 54 degrees 00 minutes
Latitude 55 degrees 00 minutes
Latitude 56 degrees 00 minutes also in 1.9 Mb Postscript or 15 kb gif
Further reading
Horology.com: Horology museums, Science
British Horological Institute
Medieval Science
About spherical astronomy by S.T. Myers, University of Pennsylvania.
Zaanse Schans Uurwerkenmuseum (in Dutch)
Back to my homepage


