How we measure the rotation velocity of a galaxy

The dynamics of dwarf galaxies is an important subject in my thesis. This page shows some of the methods I use.

Creating a velocity field.

The blue blob is a three dimensional isosurface in position-position- velocity space of a dwarf galaxy observed with the Westerbork array. See it from all directions in the animation below! If you have software to play an FLC animation, you can download this file. In this space, a rotating galaxy repesents a (curved) plane, which you saw in the animation. In the above picture, the negative (approaching, or blue shifted) velocity axis is indicated. The right hand side of the galaxy is the approaching side, the left is the receding side. The bottom of the cube is the plane of the sky. The velocity of the gas in a given line of sight (four lines of sight are drawn here) can be reconstructed, e.g. by taking the intensity weighted mean velocity. This contraction over velocity results in a map in the plane of the sky, the velocity field.

Note that the rotation velocity initially increases with distance from the centre, then levels off to become flat. This is mainly seen in bighter (bigger) galaxies, but sometimes also in faint dwarf galaxies. This particular example is a rather bright Sd type dwarf galaxy (M_B=-17). A big spiral galaxy would be M_B=-21 (that is 50 times more luminous).

In this animation you see the three-dimensional shape of a galaxy in an HI datacube. This is actual data from the Westerbork Synthesis Radio Telescope in The Netherlands. The loose blobs on one side of the galaxy are the result of unrelated emission of Galactic atomic hydrogen in the foreground.

This second animation shows the same 3 dimensional representation of the line emaission of atomic hydrogen for a dwarf galaxy which is much smaller and fainter than the previous one. The first impression is that of two big blobs which are barely connected. These two blobs represent two HI complexes in this galaxy. A more extended, faint HI halo is not visible in this animation. The rotation velocity in this galaxy is 15 km/s, only twice the velocity of the velocity of the turbulent motions.

Fitting the velocity field

This image is derived from Chapter 3, Figure 4 of my thesis

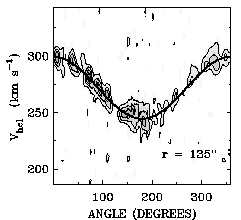
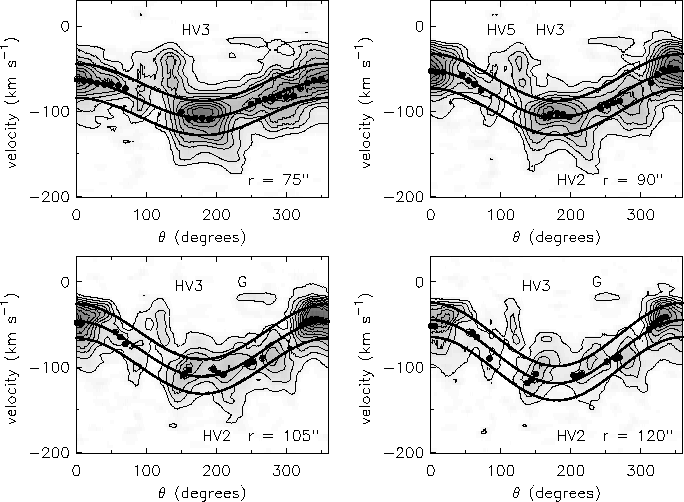
The rotation velocity as a function of distance from the centre and the angle at which we observe the galaxy, can, under certain conditions, be derived from the velocity field by a tilted ring analysis. The galaxy is divided into concentric rings (ellipses when viewed from an angle). From simple geometric arguments, the observed radial velocity along a ring is expected to vary as the cosine of the position angle. The figure below gives an example of a position angle - velocity map for a single annulus in a nearby dwarf which is considerably fainter than the two shown above. The curved line is the model velocity for that annulus. HI with an anomalous velocity can be easily identified in a diagram like this (none in this particular figure however).

Non-rotational velocities

In my thesis, I present observations of a dwarf galaxy which show HI with peculiar velocities comparable with the rotation velocity of the galaxy itself. Compare the following image with the previous image. Again, the cosine shape indicates rotation. Note however, that locally large departures from the cosine shape exist. We are confident that this gas is indeed associated with this galaxy because it coincides accurately with a bright filament of H-alpha emission. However, the contour labeled "G" in the bottom panels (also visible in the upper panels) is due to unrelated emission from our own Galaxy.

This image is derived from Chapter 7, Figure 8 of my thesis

In my thesis, and in a forthcoming paper, we address questions such as the fraction of the mass contained in the high-velocity HI gas, energetics etc.